ヒープ 🔗
ヒープ📘は、木構造📘の一種で、格納されているすべての要素の中から、最小値または最大値を持つ要素を探すことに適した構造です。
ヒープ📘という用語を、メモリ領域の分類の意味で使うことがあります。本章のテーマは、それとは関係ありません。
ヒープは、二分木📘のかたちを取ることは必須ではなく、ある節が3個以上の子を持つこともできます。ここでは話を単純にするため、子は2個以下に限定します。実際、単にヒープといったときには、子が2個以下のヒープのことを指す場合が多いです。子が2個以下になっているヒープは、二分ヒープ(バイナリヒープ)📘と呼びます。
ヒープのイメージは、次のようになります。
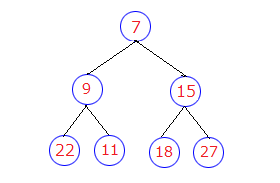 ヒープ構造
ヒープ構造
ここでは二分木のかたちにしましたが、前述したとおり、子の数はいくつでも構いません。
ヒープは、根が最小値、または最大値となるように構成します。根を最小値とした場合、ある節の値は必ずその親の値以上です。根を最大値とした場合、ある節の値は必ずその親の値以下です。
根に最小値が来るヒープを最小ヒープ、根に最大値が来るヒープを最大ヒープと呼びます。
ヒープは、根に最小値か最大値があるという特性が活かせる場面で用います。実例として、データを値の小さい順や大きい順に並び替えるソートアルゴリズムの一種であるヒープソート📘(【整列】第8章)の実現や、値が小さい順や大きい順に取り出される特殊なデータ構造である、優先度付きキュー(第10章)の実現に使われます。
根を参照する計算量はつねに O(1) という最大効率が発揮できる一方、ほかの位置への追加、削除、参照といった操作は O(log n) です。O(log n) という計算量は、二分探索木📘と変わりませんが、ヒープの特性を利用した実装(この章で取り上げる実装です)を用いると、二分探索木よりも効率的であるため、実際の性能は二分探索木よりも高くなる可能性があります。
ただし、ヒープの特性を利用した実装は制約が大きく、二分探索木のような比較的シンプルな実装よりも自由度が落ちます。たとえば、「根以外の要素を取り除く」といった実用上はあり得そうな処理を効率的に実装できません。
二分ヒープの実装 🔗
二分ヒープは、木構造の一種なので、第7章や第8章で見たような、二分木や二分探索木と同じように、節が持つ値と、子へのポインタを持つような形で実装できますが、普通はヒープならではの実装方法を用います。そうでなければ、ヒープの効率が得られません。
次のようなヒープをイメージします。○の中の数値は、格納されている値を示しているわけではなく、根から順番に連番を振ったものです。
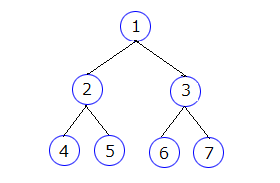 ヒープ
ヒープ
○の中の数値を観察すると、次のような法則があることが分かります。
- 左の子の連番値は、親の連番値 * 2
- 右の子の連番値は、親の連番値 * 2 + 1
- 自分の親は、自分の連番値 / 2 (余りが出たら切り捨てる)
- 自分の兄弟は、自分の連番値 - 1 か + 1
これらの法則を満たすための要件として、根の連番値が 0 ではなく 1 である必要があります。
木の形が完全二分木📘になっていなくても、要素を左側へ集めるように構成していけば、これらの法則が満たされた状態を維持できます。
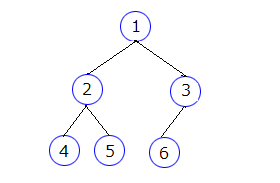 ヒープ
ヒープ
要素が1つ欠けましたが、法則が崩れることはありません。
このような法則を利用すれば、ヒープを配列で表現できます。イメージ図に登場した ○の中の数値をそのまま、配列の添字とすればいいのです。
この実装方法は、親子をつなぐポインタを使う方法と比べて、速度面でもメモリ消費量の面でも効率的です。
それでは、実際にプログラムを作ってみます。
// main.c
#include <stdio.h>
#include <string.h>
#include "heap.h"
// コマンド
enum Cmd_tag {
CMD_INSERT,
CMD_REMOVE_ROOT,
CMD_SEARCH,
CMD_PRINT,
CMD_EXIT,
CMD_NUM
};
// コマンド文字列の種類
enum CmdStr_tag {
CMD_STR_SHORT,
CMD_STR_LONG,
CMD_STR_NUM
};
// コマンドの戻り値
enum CmdRetValue_tag {
CMD_RET_VALUE_CONTINUE,
CMD_RET_VALUE_EXIT,
};
// コマンド文字列
static const char* const CMD_STR[CMD_NUM][CMD_STR_NUM] = {
{ "i", "insert" },
{ "r", "remove_root" },
{ "s", "search" },
{ "p", "print" },
{ "e", "exit" }
};
static void create_heap(void);
static void delete_heap(void);
static void print_explain(void);
static void print_blank_lines(void);
static enum CmdRetValue_tag get_cmd(void);
static enum CmdRetValue_tag cmd_insert(void);
static enum CmdRetValue_tag cmd_remove_root(void);
static enum CmdRetValue_tag cmd_search(void);
static enum CmdRetValue_tag cmd_print(void);
static enum CmdRetValue_tag cmd_exit(void);
static bool insert_elem(int value);
static bool remove_root_elem(int* value);
static bool search_elem(int value);
static void print_elem(void);
static void get_line(char* buf, size_t size);
// コマンド実行関数
typedef enum CmdRetValue_tag (*cmd_func)(void);
static const cmd_func CMD_FUNC[CMD_NUM] = {
cmd_insert,
cmd_remove_root,
cmd_search,
cmd_print,
cmd_exit
};
static Heap gHeap;
int main(void)
{
create_heap();
while( 1 ){
print_explain();
if( get_cmd() == CMD_RET_VALUE_EXIT ){
break;
}
print_blank_lines();
}
delete_heap();
return 0;
}
/*
ヒープを作成
*/
void create_heap(void)
{
gHeap = heap_create( 4 );
}
/*
ヒープを削除
*/
void delete_heap(void)
{
heap_delete( gHeap );
gHeap = NULL;
}
/*
説明文を出力
*/
void print_explain(void)
{
puts( "コマンドを入力してください。" );
printf( " ヒープに要素を挿入する: %s (%s)\n", CMD_STR[CMD_INSERT][CMD_STR_SHORT], CMD_STR[CMD_INSERT][CMD_STR_LONG] );
printf( " ヒープから根を取り除く: %s (%s)\n", CMD_STR[CMD_REMOVE_ROOT][CMD_STR_SHORT], CMD_STR[CMD_REMOVE_ROOT][CMD_STR_LONG] );
printf( " ヒープから要素を探す: %s (%s)\n", CMD_STR[CMD_SEARCH][CMD_STR_SHORT], CMD_STR[CMD_SEARCH][CMD_STR_LONG] );
printf( " ヒープの内容を表示する: %s (%s)\n", CMD_STR[CMD_PRINT][CMD_STR_SHORT], CMD_STR[CMD_PRINT][CMD_STR_LONG] );
printf( " 終了する: %s(%s)\n", CMD_STR[CMD_EXIT][CMD_STR_SHORT], CMD_STR[CMD_EXIT][CMD_STR_LONG] );
puts( "" );
}
/*
空白行を出力
*/
void print_blank_lines(void)
{
puts( "" );
puts( "" );
}
/*
コマンドを受け付ける
*/
enum CmdRetValue_tag get_cmd(void)
{
char buf[20];
get_line( buf, sizeof(buf) );
enum Cmd_tag cmd = CMD_NUM;
for( int i = 0; i < CMD_NUM; ++i ){
if( strcmp( buf, CMD_STR[i][CMD_STR_SHORT] ) == 0
|| strcmp( buf, CMD_STR[i][CMD_STR_LONG] ) == 0
){
cmd = i;
break;
}
}
if( 0 <= cmd && cmd < CMD_NUM ){
return CMD_FUNC[cmd]();
}
else{
puts( "そのコマンドは存在しません。" );
}
return CMD_RET_VALUE_CONTINUE;
}
/*
insertコマンドの実行
*/
enum CmdRetValue_tag cmd_insert(void)
{
char buf[40];
int value;
puts( "ヒープに入れる数値データを入力してください。" );
fgets( buf, sizeof(buf), stdin );
sscanf( buf, "%d", &value );
if( insert_elem( value ) ){
printf( "%d を追加しました。\n", value );
}
else{
printf( "%d の追加に失敗しました。\n", value );
}
return CMD_RET_VALUE_CONTINUE;
}
/*
remove_rootコマンドの実行
*/
enum CmdRetValue_tag cmd_remove_root(void)
{
int value;
if( remove_root_elem(&value) ){
printf( "%d を取り除きました。\n", value );
}
else{
puts( "根を取り除くことに失敗しました。" );
}
return CMD_RET_VALUE_CONTINUE;
}
/*
searchコマンドの実行
*/
enum CmdRetValue_tag cmd_search(void)
{
char buf[40];
int value;
puts( "ヒープから探し出す数値データを入力してください。" );
fgets( buf, sizeof(buf), stdin );
sscanf( buf, "%d", &value );
if( search_elem(value) ){
printf( "%d が見つかりました。\n", value );
}
else{
printf( "%d は見つかりませんでした。\n", value );
}
return CMD_RET_VALUE_CONTINUE;
}
/*
printコマンドの実行
*/
enum CmdRetValue_tag cmd_print(void)
{
print_elem();
return CMD_RET_VALUE_CONTINUE;
}
/*
exitコマンドの実行
*/
enum CmdRetValue_tag cmd_exit(void)
{
puts( "終了します。" );
return CMD_RET_VALUE_EXIT;
}
/*
要素を入れる
*/
bool insert_elem(int value)
{
return heap_insert( gHeap, value );
}
/*
要素を取り出す
*/
bool remove_root_elem(int* value)
{
return heap_remove_root( gHeap, value );
}
/*
要素を探す
*/
bool search_elem(int value)
{
return heap_search(gHeap, value);
}
/*
木の中身を出力
*/
void print_elem(void)
{
heap_print( gHeap );
}
/*
標準入力から1行分受け取る
受け取った文字列の末尾には '\0' が付加される。
そのため、実際に受け取れる最大文字数は size - 1 文字。
引数:
buf: 受け取りバッファ
size: buf の要素数
戻り値:
buf が返される
*/
void get_line(char* buf, size_t size)
{
fgets(buf, size, stdin);
// 末尾に改行文字があれば削除する
char* p = strchr(buf, '\n');
if (p != NULL) {
*p = '\0';
}
}
// heap.c
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "heap.h"
// ヒープ
struct Heap_tag {
int* data; // データ本体
size_t capacity; // 最大容量
size_t first_empty; // 空になっている最初の位置
};
#define SWAP(type,a,b) { type work = a; a = b; b = work; }
static void up_heap(Heap heap, size_t index);
static void down_root(Heap heap);
static void heap_print_node(const Heap heap, size_t index, int level);
/*
ヒープを作る
*/
Heap heap_create(size_t capacity)
{
struct Heap_tag* heap = malloc( sizeof(struct Heap_tag) );
heap->data = malloc( sizeof(int) * (capacity + 1) ); // 添字を 1 から始めるため、+ 1 して確保
heap->capacity = capacity;
heap->first_empty = 1; // 0番目は使わない
return heap;
}
/*
ヒープを削除する
*/
void heap_delete(Heap heap)
{
if( heap != NULL ){
free( heap->data );
free( heap );
}
}
/*
ヒープに要素を追加する
*/
bool heap_insert(Heap heap, int value)
{
// 容量が一杯でないか確認
if( heap->capacity < heap->first_empty ){
return false;
}
// まず、末尾に追加する
size_t index = heap->first_empty;
heap->data[index] = value;
heap->first_empty += 1;
// 適切な位置まで浮かび上がらせる
up_heap(heap, index);
return true;
}
/*
ヒープから根を取り除く
*/
bool heap_remove_root(Heap heap, int* value)
{
// ヒープが空でないか確認する
if( heap_getsize(heap) <= 0 ){
return false;
}
*value = heap->data[1];
// ヒープの最後にある要素を、先頭に移動する
heap->first_empty -= 1;
heap->data[1] = heap->data[heap->first_empty];
// 先頭に移動させた要素を、正しい位置に沈める
down_root(heap);
return true;
}
/*
ヒープから要素を探す
*/
bool heap_search(const Heap heap, int value)
{
for( int i = 1; i < heap->first_empty; ++i ){
if( heap->data[i] == value ){
return true;
}
}
return false;
}
/*
ヒープに格納されている要素数を返す
*/
size_t heap_getsize(const Heap heap)
{
return heap->first_empty - 1;
}
/*
ヒープの内容を出力する
*/
void heap_print(const Heap heap)
{
if( heap == NULL || heap_getsize(heap) <= 0 ){
return;
}
heap_print_node( heap, 1, 0 );
}
/*
ヒープの指定要素を適切な位置まで浮かび上がらせる
*/
void up_heap(Heap heap, size_t index)
{
while( index > 1 ){ // 根に到達したら終わり
size_t parent = index / 2;
if( heap->data[parent] > heap->data[index] ){
// 親との大小関係が逆なら入れ替える
SWAP( int, heap->data[parent], heap->data[index] );
// さらに親をたどる
index = parent;
}
else{
// 大小関係が正常だったら終わり
break;
}
}
}
/*
根を適切な位置まで沈める
*/
void down_root(Heap heap)
{
int index = 1; // 根から開始
while( index * 2 <= heap->first_empty ){
int child = index * 2; // 左の子の位置
// 2つの子があるなら、小さい方を使う
// 右の子の添字は、左の子の添字 + 1 である
if( child + 1 < heap->first_empty ){
if( heap->data[child] > heap->data[child + 1] ){
child = child + 1;
}
}
// 子との大小関係が逆なら、入れ替える
if( heap->data[child] < heap->data[index] ){
SWAP( int, heap->data[child], heap->data[index] );
index = child;
}
else {
break;
}
}
}
/*
ヒープの内容を出力する
*/
void heap_print_node(const Heap heap, size_t index, int level)
{
for( int i = 1; i < level; ++i ){
printf( " " );
}
if( level > 0 ){
printf( "+---" );
}
printf( "%d\n", heap->data[index] );
// 左の子
index *= 2;
if( index < heap->first_empty ){
heap_print_node( heap, index, level + 1 );
}
// 右の子
index += 1;
if( index < heap->first_empty ){
heap_print_node( heap, index, level + 1 );
}
}
// heap.h
#ifndef HEAP_TREE_H_INCLUDED
#define HEAP_TREE_H_INCLUDED
#include <stdbool.h>
// ヒープ型
typedef struct Heap_tag* Heap;
/*
ヒープを作る
引数:
capacity: ヒープの最大容量。
戻り値:
作成されたヒープ。
使い終わったら、heap_delete関数に渡して削除する。
*/
Heap heap_create(size_t capacity);
/*
ヒープを削除する
引数:
heap: ヒープ
*/
void heap_delete(Heap heap);
/*
ヒープに要素を挿入する
引数:
heap: ヒープへのポインタ
value: 挿入する要素の値
戻り値:
成功したら true、失敗したら false を返す。
*/
bool heap_insert(Heap heap, int value);
/*
ヒープから根を取り除く
引数:
heap: ヒープへのポインタ
value: 取り除かれた要素を受け取るメモリアドレス
戻り値:
成功したら true、失敗したら false を返す。
*/
bool heap_remove_root(Heap heap, int* value);
/*
ヒープから要素を探す
引数:
heap: ヒープ
value: 探し出す要素の値
戻り値:
要素が見つかれば true、見付からなければ false を返す。
*/
bool heap_search(const Heap heap, int value);
/*
ヒープに格納されている要素数を返す
引数:
heap: ヒープ
戻り値:
格納されている要素の個数。
*/
size_t heap_getsize(const Heap heap);
/*
ヒープの内容を出力する
引数:
heap: ヒープ
*/
void heap_print(const Heap heap);
#endif
初期化 🔗
これまで解説したとおり、ヒープは配列として実装します。
ここで、根の添字が 1 になるように実装すると、全体的にコードを簡潔に記述できます。そのため、添字 0 のところは未使用なままにしてあります。
配列内のどこからが未使用なのかを管理するため、first_empty というメンバがあります。
配列の 0番目の要素には、ヒープ内の要素数を入れておくなどして、使いまわすこともできます。そのような実装の実現については、練習問題に残しておきます。この方法は、配列の要素の型が整数型📘でなければなりませんが、first_emptyメンバが不要になりますし、メモリ効率の面で優れたものになります。
要素の挿入 🔗
要素の挿入は、heap_insert関数で実装しています。
まずヒープの末尾に入れてから、適切な位置まで移動させることで実現します。このとき、毎回ヒープの末尾を探索するのでは効率が悪いので、追加できる場所をつねに first_empty という変数に保存してあります。
適切な位置へ移動させる処理は、up_heap関数にあります。この処理は、自分の値と、自分の親の値を比較して、大小関係が逆転していたら、入れ替えること繰り返せば実現できます。自分の親は、「自分の添字 / 2」の位置にあることを思い出してください。
根まで到達するか、自分の値と自分の親の値の大小関係が正しい地点まで来たら完了です。
根を取り除く 🔗
根を取り除く処理は、heap_remove_root関数にあります。
まず、根の値を呼び出し元に返すため、*value への代入を済ませておきます。これを先に終わらせてしまえば、根の部分は上書きしてしまって問題ありません。
戻り値で返す仕様にしたいのなら、ローカル変数にコピーしておく必要はあるでしょう。
根を取り除くには、まず、ヒープの末尾にある要素を根の位置に上書きします。続いて、根に上書きした値を、適切な位置に移動させていきます。この処理は、down_root関数にあります。
up_heap関数とは逆で、自分の値と、2つの子の値とを比較して、大小関係が逆転していたら入れ替えます。このとき、子が1つだけしかない可能性を考慮することを忘れてはいけません。
また、子が2つある場合には、小さい方(根が一番大きくなる実装の場合は大きい方)の子と入れ替えるようにします。そうしないと最終的に、根が一番小さい(または一番大きい)状態になりません。


