二分木 | Programming Place Plus　アルゴリズムとデータ構造編【データ構造】　第７章

トップページ – アルゴリズムとデータ構造編

この章の概要 🔗

この章の概要です。


木構造 🔗

この章では、木構造（ツリー）📘というデータ構造を紹介します。連結リスト📘（第３章）と同様に、非常に重要なデータ構造です。

まず、木構造の概念図を見てください。

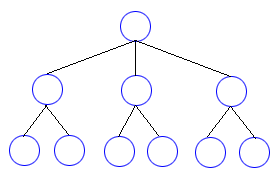
木構造

この概念図において、○ の部分を節📘（ノード）と呼びます。各節が線で結ばれていることが分かると思いますが、この線の部分を枝と呼びます。この概念図で、上下を逆さまにしてみれば、木のような形をしていることが分かると思います。これが木構造と呼ばれる理由です。

ここで、ある節から見て、その１つ下にある節のことを子と呼び、逆に１つ上の節を親と呼びます。

この辺りの用語は、家系図を見るように考えればいいです。兄弟、従弟、先祖、子孫などの用語もあります。ちなみに「兄弟」は brother ではなく sibling の方です。

一番上にある節のことを根（ルート）と呼び、一番下にある節のことを葉と呼びます。根は、つねに１つしかありませんが、葉は複数あるかもしれません。なお、葉のことを外部節（外部ノード）、葉以外の節を内部節（内部ノード）と呼ぶことがあります。

また、木には高さ（深さ）という概念があります。これは、根から一番遠い葉までに通過する枝の個数によって表現されます。

１つの節が、２つ以下の子を持つような木構造を二分木📘（バイナリツリー）と呼びます。 最初に取り上げた概念図では、根の下に子が３つあるので、これは二分木ではありません。

１つの節が３つ以上の子を持つ木構造も考えられます。このような木構造は多分木と呼ばれます。

１つの節が１つしか子を持たない場合もありえます。これはもはや木のような形にはなりませんが、これでも木構造とみなすことはできます。このような形の木構造は、もはや連結リストと同じかたちをしています。

木構造の利点は、格納されているデータを見つける効率の良さにあるのですが、連結リストと同じかたちになってしまった木構造ではその利点が消えてしまいます。もはや連結リストと同じものなのですから、先頭から要素を１つ１つ辿っていくしかなくなるためです。

木構造に要素を追加していくときに、節を置く位置を誤ると、このような状態になってしまうことがあります。木構造の性能上の利点をきちんと得るには、この問題への対策を考える必要があります。

木構造が連結リストのような形になってしまう問題については、次の第８章で取り上げることにして、本章ではきちんと二分木になっている前提の話をします。

二分木 🔗

二分木とは、葉以外のすべての節が、２つ以下の子を持つような木構造のことです。もし、必ず２つの子を持つようならば、全二分木📘と呼ばれます。さらに、どの葉も同じ深さにある場合は、完全二分木📘と呼ばれます。

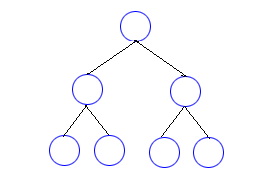
概念図は次のようになります。

二分木

この概念図は、葉以外のすべての節が子を必ず２つずつ持っており、どの葉も同じ深さにあるので、完全二分木になっていると言えます。

Ｃ言語のプログラムでは、二分木を次のように表現できます。

struct Node_tag {
    int                   value;    // この節のデータ
    struct Node_tag*      left;     // 左の子へのポインタ
    struct Node_tag*      right;    // 右の子へのポインタ
};

この構造体は１つの節を表します。通常、節ごとに動的にメモリ割り当てを行い、その都度、left と right を適切に設定、あるいは更新します（連結リストと同じ感覚で考えればいいです）。

子がない場合は、left や right には、NULL を入れておけばよいでしょう。

value というメンバは、この節に置かれた具体的なデータを表すもので、もちろん int型である必要はなく、任意のデータを任意の数だけ置けます。

この構造体をよく観察すると、双方向連結リスト（第４章）の構造体とまったく同じ形をしていることが分かります。違いは、next と prev という名前のポインタが、left と right に変わっただけです。構造体の形は一緒でも、それをどう扱うかによって、実現できることはまったく異なります。

この構造体を見ると分かるように、親に向かうポインタを持っていません。もちろん、ポインタを１つ付け加えれば、親をたどれますが、その必要性がないのなら不要です。木構造は、根からその子をたどることを繰り返して、目的の節へ行き着くというように利用することが多く、親をたどる必要性がない場合もよくあります。


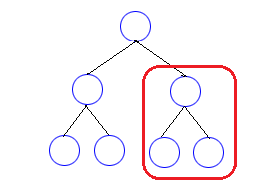
再帰的な性質 🔗

次の図は、二分木の概念図に、赤い枠を加えたものです。

二分木

二分木の一部分を囲っていますが、この囲まれた部分だけを観察してみると、その部分もやはり二分木になっていることが分かります。

このように、木構造はその一部分だけを取り出してみても、やはり木構造の形をしているという特徴があります。ここで、一部分の木のことを部分木と呼びます。

この概念図の場合、全体としての根の右側にある部分木を囲っていますが、この場合、根に対して右部分木と呼びます。左側にあれば左部分木と呼ばれます。

もっと大きな木構造であれば、部分木の中にさらに部分木が、その中にさらに部分木があるという構造になります。このように、自分自身の一部が、自分自身と同じ形状をしているような構造は、再帰的な構造と呼ばれます。

データ構造が再帰的になっているのであれば、プログラムでも再帰処理を活用しやすくなります。次の項で、すべての節を調べつくす処理を取り上げますが、ここでは再帰処理を利用しています。

走査 🔗

二分木に含まれるすべての節を調べたいとします。このような処理を、走査（トラバース）と呼びます。ここで重要な点は、「すべてをもらさず」「同じものを重複せず」に調べつくすことです。

二分木に対する走査の方法には、大きく分けると、深さ優先探索と幅優先探索の２つがあります。前者はさらに、行きがけ順探索、通りがけ順探索、帰りがけ順探索に分類できます。これらは、調べる節の順序が異なります。

深さ優先探索では、根から始めて、葉に行き着くまで子をたどっていきます。葉まで行き着いたら、その親に戻り、先ほど辿った側ではないもう一方の子を調べに行き、やはり葉までたどります。これを繰り返せば、いずれすべての節を調べられます。

行きがけ順探索、通りがけ順探索、帰りがけ順探索の違いは、根とその２つの子をどんな順序で調べるかです。

もう１つの方法である幅優先探索は、まず根を調べ、次に１つ深い階層の左部分木、右部分木を調べます。１つの階層の節をすべて網羅してから、次の階層へ降りることを繰り返します。

それでは実際に、それぞれの走査を実装してみましょう。

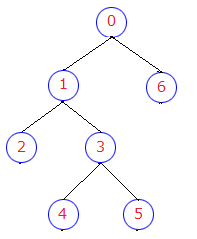
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define SIZE_OF_ARRAY(array)    (sizeof(array)/sizeof(array[0]))


// コマンド
enum Cmd_tag {
    CMD_PRE_ORDER,
    CMD_IN_ORDER,
    CMD_POST_ORDER,
    CMD_EXIT,

    CMD_NUM
};

// コマンド文字列の種類
enum CmdStr_tag {
    CMD_STR_SHORT,
    CMD_STR_LONG,

    CMD_STR_NUM
};

// コマンドの戻り値
enum CmdRetValue_tag {
    CMD_RET_VALUE_CONTINUE,
    CMD_RET_VALUE_EXIT,
};

// コマンド文字列
static const char* const CMD_STR[CMD_NUM][CMD_STR_NUM] = {
    { "r", "pre" },
    { "i", "in" },
    { "p", "post" },
    { "e", "exit" }
};


// 二分木
struct Node_tag {
    int                   value;
    struct Node_tag*      left;
    struct Node_tag*      right;
};
typedef struct Node_tag* BinaryTree;


static BinaryTree create_binary_tree(void);
static void delete_binary_tree(BinaryTree tree);
static void print_explain(void);
static void print_blank_lines(void);
static enum CmdRetValue_tag get_cmd(void);
static enum CmdRetValue_tag cmd_pre_order(void);
static enum CmdRetValue_tag cmd_in_order(void);
static enum CmdRetValue_tag cmd_post_order(void);
static enum CmdRetValue_tag cmd_exit(void);
static void pre_order(BinaryTree tree);
static void in_order(BinaryTree tree);
static void post_order(BinaryTree tree);
static void get_line(char* buf, size_t size);


// コマンド実行関数
typedef enum CmdRetValue_tag (*cmd_func)(void);
static const cmd_func CMD_FUNC[CMD_NUM] = {
    cmd_pre_order,
    cmd_in_order,
    cmd_post_order,
    cmd_exit
};


static BinaryTree gTree;


int main(void)
{
    gTree = create_binary_tree();

    while( 1 ){
        print_explain();

        if( get_cmd() == CMD_RET_VALUE_EXIT ){
            break;
        }

        print_blank_lines();
    }

    delete_binary_tree( gTree );

    return 0;
}

/*
    二分木を作成

    ここでは、
             0
            / \
           1   6
          / \
         2   3
            / \
           4   5

    という形の二分木を作っている。
*/
BinaryTree create_binary_tree(void)
{
    BinaryTree node[7];

    for( size_t i = 0; i < SIZE_OF_ARRAY(node); ++i ){
        node[i] = malloc( sizeof(struct Node_tag) );
        node[i]->value = (int)i;
    }

    node[0]->left = node[1];
    node[0]->right = node[6];

    node[1]->left = node[2];
    node[1]->right = node[3];

    node[2]->left = NULL;
    node[2]->right = NULL;

    node[3]->left = node[4];
    node[3]->right = node[5];

    node[4]->left = NULL;
    node[4]->right = NULL;

    node[5]->left = NULL;
    node[5]->right = NULL;

    node[6]->left = NULL;
    node[6]->right = NULL;

    return node[0];
}

/*
    二分木を削除
*/
void delete_binary_tree(BinaryTree tree)
{
    if( tree == NULL ){
        return;
    }

    delete_binary_tree( tree->left );
    delete_binary_tree( tree->right );
    free( tree );
}

/*
    説明文を出力
*/
void print_explain(void)
{
    puts( "コマンドを入力してください。" );
    printf( "　行きがけ順探索: %s (%s)\n", CMD_STR[CMD_PRE_ORDER][CMD_STR_SHORT], CMD_STR[CMD_PRE_ORDER][CMD_STR_LONG] );
    printf( "　通りがけ順探索: %s (%s)\n", CMD_STR[CMD_IN_ORDER][CMD_STR_SHORT], CMD_STR[CMD_IN_ORDER][CMD_STR_LONG] );
    printf( "　帰りがけ順探索: %s (%s)\n", CMD_STR[CMD_POST_ORDER][CMD_STR_SHORT], CMD_STR[CMD_POST_ORDER][CMD_STR_LONG] );
    printf( "　終了する: %s(%s)\n", CMD_STR[CMD_EXIT][CMD_STR_SHORT], CMD_STR[CMD_EXIT][CMD_STR_LONG] );
    puts( "" );
}

/*
    空白行を出力
*/
void print_blank_lines(void)
{
    puts( "" );
    puts( "" );
}

/*
    コマンドを受け付ける
*/
enum CmdRetValue_tag get_cmd(void)
{
    char buf[20];
    get_line( buf, sizeof(buf) );

    enum Cmd_tag cmd = CMD_NUM;
    for( int i = 0; i < CMD_NUM; ++i ){
        if( strcmp( buf, CMD_STR[i][CMD_STR_SHORT] ) == 0
         || strcmp( buf, CMD_STR[i][CMD_STR_LONG] ) == 0
        ){
            cmd = i;
            break;
        }
    }

    if( 0 <= cmd && cmd < CMD_NUM ){
        return CMD_FUNC[cmd]();
    }
    else{
        puts( "そのコマンドは存在しません。" );
    }

    return CMD_RET_VALUE_CONTINUE;
}

/*
    preコマンドの実行
*/
enum CmdRetValue_tag cmd_pre_order(void)
{
    puts( "行きがけ順探索で、節の値を書き出します。" );
    pre_order( gTree );

    return CMD_RET_VALUE_CONTINUE;
}

/*
    inコマンドの実行
*/
enum CmdRetValue_tag cmd_in_order(void)
{
    puts( "通りがけ順探索で、節の値を書き出します。" );
    in_order( gTree );

    return CMD_RET_VALUE_CONTINUE;
}

/*
    postコマンドの実行
*/
enum CmdRetValue_tag cmd_post_order(void)
{
    puts( "帰りがけ順探索で、節の値を書き出します。" );
    post_order( gTree );

    return CMD_RET_VALUE_CONTINUE;
}

/*
    exitコマンドの実行
*/
enum CmdRetValue_tag cmd_exit(void)
{
    puts( "終了します。" );

    return CMD_RET_VALUE_EXIT;
}

/*
    行きがけ順探索でトラバース
*/
void pre_order(BinaryTree tree)
{
    if( tree == NULL ){
        return;
    }

    printf( "%d\n", tree->value );
    pre_order( tree->left );
    pre_order( tree->right );
}

/*
    通りがけ順探索でトラバース
*/
void in_order(BinaryTree tree)
{
    if( tree == NULL ){
        return;
    }

    in_order( tree->left );
    printf( "%d\n", tree->value );
    in_order( tree->right );
}

/*
    帰りがけ順探索でトラバース
*/
void post_order(BinaryTree tree)
{
    if( tree == NULL ){
        return;
    }

    post_order( tree->left );
    post_order( tree->right );
    printf( "%d\n", tree->value );
}

/*
    標準入力から１行分受け取る

    受け取った文字列の末尾には '\0' が付加される。
    そのため、実際に受け取れる最大文字数は size - 1 文字。

    引数：
        buf:    受け取りバッファ
        size:   buf の要素数
    戻り値：
        buf が返される
*/
void get_line(char* buf, size_t size)
{
    fgets(buf, size, stdin);

    // 末尾に改行文字があれば削除する
    char* p = strchr(buf, '\n');
    if (p != NULL) {
        *p = '\0';
    }
}

二分木に持たせるデータは、create_binary_tree関数の中で固定的に作っています。図にすると、次のような形になっています。

二分木

なんだか適当につくっていると思われたかもしれません。木構造へ適切に要素を追加していくには、それなりの手順が必要です。この話は、次の章で取り上げることにして、ここではこれでよしとしておきます。

この二分木に対して、行きがけ順探索をおこなうと、

行きがけ順探索で、節の値を書き出します。
0
1
2
3
4
5
6

通りがけ順探索をおこなうと、

通りがけ順探索で、節の値を書き出します。
2
1
4
3
5
0
6

帰りがけ順探索をおこなうと、

帰りがけ順探索で、節の値を書き出します。
2
4
5
3
1
6
0

というように出力されます。

それぞれの走査は、行きがけ順探索は pre_order関数、通りがけ順探索は in_order関数、帰りがけ順探索は post_order関数の中で行っています。幅優先探索については、練習問題に残しておくことにします。

これらの実装を見ると分かるように、すべて再帰処理📘（Ｃ言語編第５３章参照）が行われています。

「再帰的な性質」のところで説明したように、木構造は再帰的な構造をしており、再帰処理を活用すれば、短いコードで大きな仕事を行えます。これらの走査関数がいずれも、非常に短いコードで実装されていることが分かると思います。

最後に、delete_binary_tree関数も確認しておきましょう。create_binary_tree関数の中で二分木を作るとき、各節を malloc関数で確保したメモリに作っているので、削除するときには free関数を呼ぶ必要があります。問題はそれを呼ぶ順番です。

子よりも先に親を解放📘してしまうと、親が持っていた left と right へのアクセスは不正なものになってしまうので、必ず先に子を解放しなければなりません。そのためには、帰りがけ順探索と同じ順序で処理をおこなうのが適切です。帰りがけ順探索ならば、「左の子→右の子→親」の順番でアクセスできるからです。

これらの走査方法のどれかがはっきりと優れているということはありませんが、効率良く目的の処理をおこなうためにはどれが適切なのかを判断できる必要はあるので、どういう順序で節を参照することになるのか理解しておきましょう。

まとめ 🔗

この章では、木構造の概要を学び、代表例として二分木を取り上げました。しかし、この章の内容だけでは、いまいち具体性がなくて明らかに不十分でしょう。

木構造にはいくつか代表的な応用があり、実戦の中ではそういったやや複雑な木構造を用いることが多くあります。その中でももっとも代表的な二分探索木📘を次章で解説します。


練習問題 🔗

問題①　二分木の高さを返す関数を作成してください。

問題②　幅優先探索による走査をおこなう関数を実装してください。


解答ページはこちら。


参考リンク 🔗


更新履歴 🔗

≪さらに古い更新履歴≫


前の章へ　（第６章　キュー）

次の章へ　（第８章　二分探索木）

アルゴリズムとデータ構造編のトップページへ

Programming Place Plus のトップページへ

はてなブックマーク に保存 Pocket に保存 Facebook でシェア
X で ポスト／フォロー LINE で送る noteで書く
rss1.0 取得ボタン RSS 管理者情報 プライバシーポリシー
先頭へ戻る