メモリを浪費しない実装 🔗
先ほどのサンプルプログラムでは、ソート対象のデータ列の2倍程度のメモリを使ってしまう問題があります。この問題を解決してみます。
問題は、heap_create関数の中で確保している配列です。
/*
ヒープを作る
*/
Heap heap_create(size_t capacity)
{
struct Heap_tag* heap = malloc( sizeof(struct Heap_tag) );
heap->data = malloc( sizeof(int) * (capacity + 1) ); // 添字を 1 から始めるため、+ 1 して確保
heap->capacity = capacity;
heap->first_empty = 1; // 0番目は使わない
return heap;
}この配列 (heap->data) は、あくまで作業用です。ソート対象の要素がいったんここにすべて集められてヒープを構築し、その後、すべて取り出されます。
もし、“いったんここにすべて集め” ずに、ソート対象の配列の中だけを使ってヒープを構築できれば、メモリ使用量は一気に半分になります。
ソート対象の配列は main.c にあるので、とりあえずの方針として、heap.c と heap.h にあるコードのいくらかを main.c に移し替えます。
まず、ヒープをあらわす構造体📘をもってきます。
// ヒープ
struct Heap_tag {
int* data; // データ本体
size_t capacity; // 最大容量
size_t first_empty; // 空になっている最初の位置
};
typedef struct Heap_tag Heap;ソート対象の配列自体をヒープにしたいのですから、data メンバはソート対象の配列を指し示すようにします。
int array[] = {7, 2, 9, 6, 4, 3, 8, 1, 5};
Heap heap;
heap.data = array;
heap.capacity = SIZE_OF_ARRAY(array);
heap.first_empty = SIZE_OF_ARRAY(array);heap_create関数のときは、指定された要素数よりも 1つ余分に確保していました。これは、添字の計算を楽にするために、0 のところを使わないようにするためです。しかし、ソート対象配列の 0番目の要素には、すでにデータが入ってしまっていることが多いでしょう。0番目も普通に要素が入っているものとして扱うことにします。
heap.c の処理を使った実装のときは、ヒープに要素を1つ1つ挿入していましたが、今回はその過程がなくなります。すでにデータが入っている配列を指すので、ヒープは一杯になっているとみなします。first_empty メンバの値は、最後の要素のさらに後ろ、つまり、空きはありません。
さて、この時点ではヒープの要件をまったく満たしていません。ヒープは、根が最小値、または最大値となるように構成しなければなりません。根を最小値とした場合、ある節の値は必ずその親の値以上です。根を最大値とした場合、ある節の値は必ずその親の値以下です。
heap.c では、heap_insert関数の中で適切な位置を見つける処理を行っていますが、今回は、要素を挿入することがないので、どこか別のタイミングで、同じような処理を書く必要があります。
タイミングについては簡単です。さっさとヒープとして正しい状態にしなければなりませんから、さきほど、Heap構造体を初期化した直後に書きます。
問題は方法です。heap_insert関数では、挿入する要素をいったん末尾に置き、その後、適切な位置を探していました。イメージとしては、木構造📘の一番深いところに置いてから、適切な位置まで浮かび上がらせるということです。しかし今回は、末尾の位置にはじめから要素が置かれていますから、この方法をマネすることはできません。
そこで考え方を反対にして、要素を適切な位置まで沈めるようにします。このような操作は heap.c の down_root関数にすでにあります。down_root関数は、ヒープから要素を取り除くときに使われています。ヒープでは取り除く要素がつねに根にありますから、取り除いたあと、根の部分が空くことになります。そこで、末尾にある要素をその空いた位置に移動させ、その要素を適切な位置まで沈めるという操作を行っていました。
これをそのまま利用すれば、根の要素を適切な位置へ移動できます。
down_root(&heap);しかし、この操作を行っても、根の要素にとって本当に適切な位置が、やはり根の位置だった、ということはあり得ますから、必ずしも根の要素が移動するわけではありません。そのため、この処理を何度繰り返しても、一向に要素が動かず、ヒープにならないという事態が起こり得ます(高確率でそうなるでしょう)。
そこで、根の位置を変えながら、down_root関数を繰り返し呼ぶようにします。根の位置を変えるというのは変な話なようですが、木構造は再帰的なかたちをしていることを思い出しましょう。つまり、部分部分を1つの木(部分木)とみなせば、根はいくつもあります。
具体的にどうすればいいかというと、まず、一番深く、一番右側にある根を探して、その位置に対して down_root関数の処理を適用します。その後は、左側へ移動、なければ上(親)の段へ移動、というように動きながらそのつど、down_root関数の処理を適用します。これを、木構造全体の根に到達するまで繰り返します。
「一番深く、一番右側にある根」の位置は、ヒープの性質を利用すれば簡単にわかります。ヒープには次の性質があるのでした(【データ構造】第9章)。
- 左の子の連番値は、親の連番値 * 2
- 右の子の連番値は、親の連番値 * 2 + 1
- 自分の親は、自分の連番値 / 2 (余りが出たら切り捨てる)
- 自分の兄弟は、自分の連番値 - 1 か + 1
連番値とは、全体の根を 1 としたときの添字のことです。今回は、添字を 0 から始めなければならないので、次のように読み替えます。
- 左の子の連番値は、親の連番値 * 2 + 1
- 右の子の連番値は、親の連番値 * 2 + 2
- 自分の親は、(自分の連番値 - 1) / 2 (余りが出たら切り捨てる)
- 自分の兄弟は、自分の連番値 - 1 か + 1
末尾の要素の位置は分かっているので(heap.first_empty - 1)、その親が「一番深く、一番右側にある根」です。よって、((heap.first_empty - 1) - 1) / 2 で求められます。少し整理すると、(heap.first_empty - 2) / 2 です。
down_root関数の引数には、根とみなす要素の位置を指定できませんから、引数を都合のいいように変えます。位置が指定できるのなら、もはや root と呼ぶのもおかしいので、関数名も down_heap に変えます。
/*
ヒープの指定要素を適切な位置まで沈める
引数:
heap: ヒープへのポインタ
root: 根の位置
end: 末尾の位置
*/
void down_heap(Heap* heap, int root, int end);そのうえで、次のように繰り返せば、ヒープを構築できます。「左側へ移動、なければ上の段へ移動」という操作は、変数 root をデクリメント📘するだけで実現できます。
for( int root = ((int)(heap.first_empty) - 2) / 2; root >= 0; --root) {
down_heap( &heap, root, heap.first_empty - 1 );
}heap.first_empty が size_t型(符号無し整数型📘)なので、int型へのキャスト📘をしておかないと「-2」した結果が巨大な正の数になってしまい失敗します。ヒープの章で使ったコードが size_t型になっているので、それに合わせたコードですが、heap.first_empty を int型にするのでも構いません。
この処理を終えた時点で、ヒープとして正しい並びになっています。概念図であらわすと、以下のようになります。
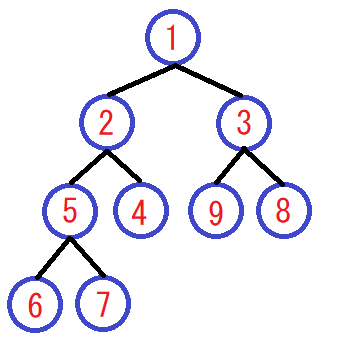
根に一番小さい値があり、子は親以上の値を持つという要件は満たされています。しかし、配列をソートするという、本来の目的が達成されたわけではありません。この時点で、配列は次のようになっており、ソートできていません。
1 2 3 5 4 9 8 6 7ヒープソートの基本手順は、この章の最初に書いたとおり「ソートしたいデータ列をヒープへすべて挿入し、あとは順次取り出す」です。ここまでに前半部分は終わりました。あとは後半部分を実行すれば、ソート済みの配列が得られます。
「順次取り出す」のところで取り出す値は(根のことなので)、最小値(あるいは最大値)です。しかし、対象の配列がソートしたい配列そのものなので、要素を実際に取り出してしまうわけにはいきません。そこで、取り出す代わりに、配列の末尾にある要素と交換すればいいでしょう。
しかし、単に交換するだけだと、根の位置に最小値(あるいは最大値)ではない値が置かれてしまいます。そこでここでも、down_heap関数を呼びます。交換によって根の位置にやってきた要素を、down_heap の処理にかけてやれば、適切な位置へ沈んでいき、ヒープの状態が保たれます。
そうしたらまた、根と末尾(本当の末尾は先ほど定まったので、今度は1つ手前)を交換し、down_heap を呼び、また根と末尾(の2つ手前)を交換し・・・と繰り返せば、ソートを実現できます。
void sort_heap(Heap* heap)
{
int end = (int)heap->first_empty - 1;
while( end >= 1 ){
SWAP(int, heap->data[0], heap->data[end]);
end--;
down_heap( heap, 0, end );
}
}ここまでの話をすべて踏まえて、ヒープソートをおこなうプログラムは次のようになります。
#include <stdio.h>
#define SIZE_OF_ARRAY(array) (sizeof(array)/sizeof(array[0]))
#define SWAP(type,a,b) { type work = a; a = b; b = work; }
// ヒープ
struct Heap_tag {
int* data; // データ本体
size_t capacity; // 最大容量
size_t first_empty; // 空になっている最初の位置
};
typedef struct Heap_tag Heap;
static void heap_sort(int* array, size_t size);
static void down_heap(Heap* heap, size_t root, size_t end);
static void sort_heap(Heap* heap);
static void print_array(const int* array, size_t size);
int main(void)
{
int array[] = {7, 2, 9, 6, 4, 3, 8, 1, 5};
print_array( array, SIZE_OF_ARRAY(array) );
heap_sort( array, SIZE_OF_ARRAY(array) );
print_array( array, SIZE_OF_ARRAY(array) );
return 0;
}
/*
ヒープソート (昇順)
*/
void heap_sort(int* array, size_t size)
{
Heap heap;
heap.data = array;
heap.capacity = size;
heap.first_empty = size;
// ヒープを再構成
for( int root = ((int)(heap.first_empty) - 2) / 2; root >= 0; --root) {
down_heap( &heap, root, heap.first_empty - 1 );
}
// ヒープ内をソートする
sort_heap( &heap );
}
/*
ヒープの指定要素を適切な位置まで沈める
*/
void down_heap(Heap* heap, size_t root, size_t end)
{
while( root * 2 + 1 <= end ){
size_t child = root * 2 + 1; // 左の子の位置
// 2つの子があるなら、小さい方を使う
// 右の子の添字は、左の子の添字 + 1 である
if( child + 1 <= end ){
if( heap->data[child] > heap->data[child + 1] ){
child = child + 1;
}
}
// 子との大小関係が逆なら、入れ替える
if( heap->data[child] < heap->data[root] ){
SWAP( int, heap->data[child], heap->data[root] );
root = child;
}
else {
break;
}
}
}
/*
ヒープ内をソートする
*/
void sort_heap(Heap* heap)
{
int end = (int)heap->first_empty - 1;
while( end >= 1 ){
SWAP(int, heap->data[0], heap->data[end]);
end--;
down_heap( heap, 0, end );
}
}
/*
配列の要素を出力
*/
void print_array(const int* array, size_t size)
{
for( size_t i = 0; i < size; ++i ){
printf( "%d ", array[i] );
}
printf( "\n" );
}実行結果:
7 2 9 6 4 3 8 1 5
9 8 7 6 5 4 3 2 1これで、メモリを浪費せずにヒープソートを実現できました。
ただ、ソートが昇順📘でなくて、降順で行われています。もちろんそれでいいならいいのですが、やはり昇順にしたいことが多いので、どうにかしなければなりません。
これはヒープを構築する際の大小関係の判定を逆にすれば修正できます。具体的には、down_heap関数内の2つの if文の条件式📘を書き換えます(★のコメントが入っているところ)。
/*
ヒープの指定要素を適切な位置まで沈める
*/
void down_heap(Heap* heap, size_t root, size_t end)
{
while( root * 2 <= end ){
size_t child = root * 2 + 1; // 左の子の位置
// 2つの子があるなら、大きい方を使う
// 右の子の添字は、左の子の添字 + 1 である
if( child + 1 <= end ){
if( heap->data[child] < heap->data[child + 1] ){ // ★
child = child + 1;
}
}
// 子との大小関係が逆なら、入れ替える
if( heap->data[child] > heap->data[root] ){ // ★
SWAP( int, heap->data[child], heap->data[root] );
root = child;
}
else {
break;
}
}
}